Défnition : Du latin: torus "coussin, bourrelet".

 

 

 

1- Un tore désigne la surface engendrée par la rotation d'un cercle autour d'une droite. La droite, appelée axe du tore, appartient au plan du cercle, mais ne coupe pas le cercle.

 

 

 

 

 

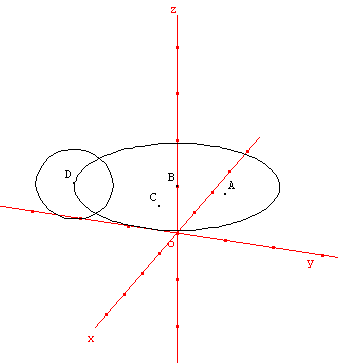
2-Surface engendrée par la rotation d'un cercle autour d'un axe situé dans le plan du cercle et ne coupant pas ce dernier.

Soit "r" le rayon du cercle et "R" la distance du centre C(du tore) à l'axe de rotation :

 

 

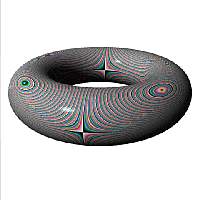
-si R>r le tore est dit "ouvert" et ressemble à une chambre à air.

 

 

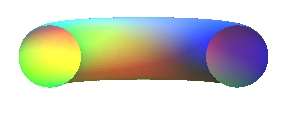
-si R=r le tore est "à collier nul"

 

 

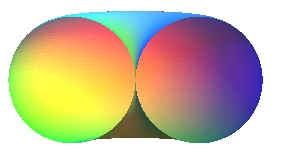
-si R<r le tore est dit croisé et ressemble à une citrouille. Les mathématiciens ne sont pas d'accord sur ce point : certains disent que le tore croisé n'est pas un tore ce qui est facilement expliquable puisque dans ce cas le cercle coupe l'axe du tore ce qui est contraire à la définition ; mais d'autres affirment que le tore croisé est bien un tore puisque c'est bel et bien une surface engendrée par la rotation d'un cercle autour d'une droite bien que le cercle coupe cette droite.

 

 

 

 

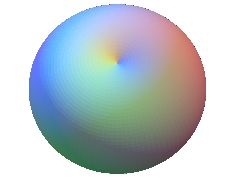
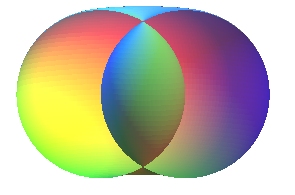
On voit ici que rien que la définition du tore pose des problèmes puisque les mathématiciens ne sont pas d'accord sur tous les points et il n'y a aucune des deux versions qui soit reconnue universalement.