Les coupes du tore :

 

 

Résultats de coupes d'un tore selon différents plans :

-la coupe verticale:
soit un plan coupant un tore verticalement ( c'est à dire que le plan passe par la verticale représentant l'axe du tore ), l'intersection entre ce plan et le tore donnent deux cercles de rayon r

 

 

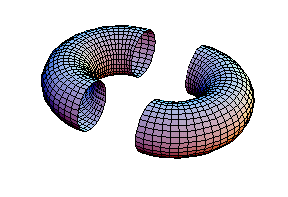
-la coupe horizontale:
soit un plan coupant un tore horizontalement ( c'est à dire le plan perpendicullaire à l'axe du tore passant par son centre ), l'intersection entre ce plan et le tore forme deux cercles concentriques : les cercles intérieurs et extérieurs.

 

 

 

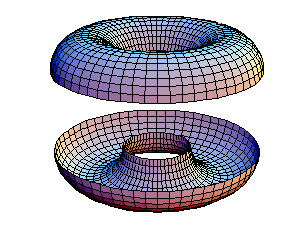
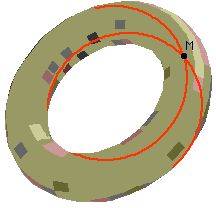
-la coupe bitangente (cercles de Villarceau):
soit un point M quelconque sur la surface du tore,lorsque le point M admet un plan bitangent (tangent dessus-dessous), on obtient deux cercles (dits de Villarceau) par intersection de ce plan avec le tore.

 

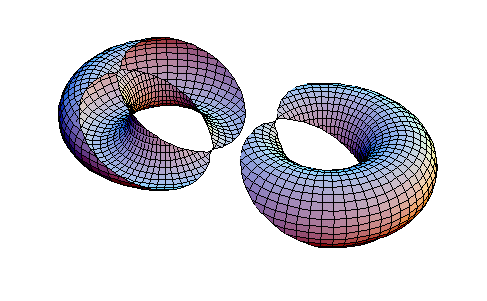
Ces cercles étaient déjà connus des architectes depuis longtemps puisqu'on les retrouve dans l'escalier du musée de la cathédrale de Strasbourg : oeuvre de Thomas Uhlberger vers 1578/82 (le "Théorème sur le tore" de Villarceau n'est publié qu'en 1848) durant la construction de la partie ouest du bâtiment de l'Oeuvre Notre-Dame.